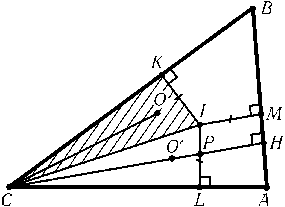
Пусть 90^o$\geq$$\alpha$$\geq$$\beta$$\geq$$\gamma$. Тогда CH — наибольшая высота. Центры вписанной и описанной окружностей обозначим через Iи O, точки касания вписанной окружности со сторонами BC,CA,AB — через K,L,Mсоответственно (рис.). Докажем сначала, что точка Oлежит внутри треугольника KCI. Для этого достаточно доказать, что CK$\geq$KBи $\angle$BCO$\leq$BCI. Ясно, что CK=rctg($\gamma$/2)$\geq$rctg($\beta$/2) =KBи 2$\angle$BCO= 180^o-$\angle$BOC= 180^o- 2$\alpha$$\leq$180^o-$\alpha$-$\beta$=$\gamma$= 2$\angle$BCI. Так как $\angle$BCO= 90^o-$\alpha$=$\angle$ACH, при симметрии относительно CIпрямая COпереходит в прямую CH. Пусть O' — образ точки Oпри этой симметрии, P — точка пересечения CHи IL. Тогда CP$\geq$CO'=CO=R. Остается доказать, что PH$\geq$IM=r. Это следует из того, что $\angle$MIL= 180^o-$\alpha$$\geq$90^o.

Ответ задачи отсутствует