Задача
а) Выпуклые многоугольники A1...Anи B1...Bnтаковы, что все их соответственные стороны, кроме A1Anи B1Bn, равны и $\angle$A2$\geq$$\angle$B2,...,$\angle$An - 1$\geq$$\angle$Bn - 1, причем хотя бы одно из неравенств строгое. Докажите, что A1An>B1Bn. б) Соответственные стороны неравных многоугольников A1...Anи B1...Bnравны. Запишем возле каждой вершины многоугольника A1...Anзнак разности $\angle$Ai-$\angle$Bi. Докажите, что при n$\geq$4 соседних вершин с разными знаками будет по крайней мере четыре пары. (Вершины с нулевой разностью выбрасываются из рассмотрения: две вершины, между которыми стоят только вершины с нулевой разностью, считаются соседними.)
Решение
а) Предположим сначала, что $\angle$Ai>$\angle$Bi, а для всех остальных рассматриваемых пар углов имеет место равенство. Расположим многоугольники так, чтобы вершины A1,...,Aiсовпали с B1,...,Bi. В треугольниках A1AiAnи A1AiBnстороны AiAnи AiBnравны и $\angle$A1AiAn>$\angle$A1AiBn, поэтому A1An>A1Bn. Если же не равны несколько углов, то многоугольники A1...Anи B1...Bnможно включить в цепочку многоугольников, последовательные члены которой такие, как в разобранном выше случае. б) При полном обходе многоугольника знак минус меняется на знак плюс столько же раз, сколько происходит обратная смена знака. Поэтому число пар соседних вершин с разными знаками четно. Остается проверить, что число изменений знака не может быть равно двум (число изменений знака не равно нулю, так как сумма углов обоих многоугольников одна и та же).
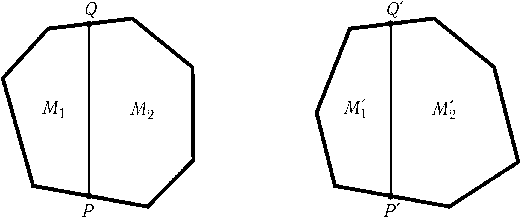
Предположим, что число изменений знака равно двум. Пусть Pи Q, P'и Q' — середины сторон многоугольников A1...Anи B1...Bn, на которых происходит смена знака. К парам многоугольников M1и M1', M2и M2' (рис.) можно применить утверждение задачи а); в одном случае получим PQ>P'Q', а в другом PQ<P'Q', чего не может быть.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь