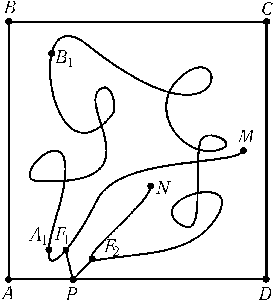
Пусть Mи N — концы ломаной. Будем идти по ломаной из Mв N. Пусть A₁ — первая из встретившихся нам точек ломаной, удаленных от какой-либо вершины квадрата на расстояние 0,5. Рассмотрим вершины квадрата, соседние с этой вершиной. Пусть B₁ — первая после A₁точка ломаной, удаленная от одной из этих вершин на расстояние 0,5. Вершины квадрата, ближайшие к точкам A₁и B₁, обозначим Aи Bсоответственно (рис.). Часть ломаной от Mдо A₁обозначим через L₁, от A₁до N — через L₂. Пусть Xи Y — множества точек, лежащих на ADи удаленных не более чем на 0,5 от L₁и L₂соответственно. По условию Xи Yпокрывают всю сторону AD. Ясно, что Aпринадлежит X, а Dне принадлежит X, поэтому Dпринадлежит Y, т. е. оба множества Xи Yне пусты. Но каждое из них состоит из нескольких отрезков, поэтому они должны иметь общую точку P. Следовательно, на L₁и L₂существуют точки F₁и F₂, для которых PF₁$\leq$0, 5 и PF₂$\leq$0, 5. Докажем, что F₁и F₂ — искомые точки. В самом деле, F₁F₂$\leq$F₁P+PF₂$\leq$1. С другой стороны, идя в F₂из F₁, мы должны пройти через точку B, а F₁B₁$\geq$99 и F₂B₁$\geq$99, так как точка B₁удалена от стороны BCне больше чем на 0,5, а F₁и F₂удалены от стороны ADне больше чем на 0,5.

Ответ задачи отсутствует