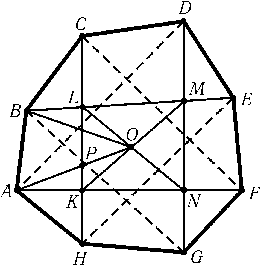
а) Обозначим точки пересечения диагоналей ADи CF, CFи BE, BEи ADчерез P,Q,Rсоответственно (рис.). Четырехугольники ABCPи CDEQне имеют общих внутренних точек, так как стороны CPи QCлежат на прямой CF, а отрезки ABи DE — по разные стороны от нее. Аналогично четырехугольники ABCP,CDEQи EFARне имеют попарно общих внутренних точек. Поэтому сумма их площадей не превосходит S. Следовательно, сумма площадей треугольников ABP,BCP,CDQ,DEQ,EFR,FARне превосходит S, т. е. площадь одного из них, например ABP, не превосходит S/6. Точка Pлежит на отрезке CF, поэтому либо точка C, либо точка Fудалена от прямой ABне больше, чем точка P. Следовательно, либо S_ABC$\leq$S_ABP$\leq$S/6, либо S_ABF$\leq$S_ABP$\leq$S/6. б) Пусть ABCDEFGH — выпуклый восьмиугольник (рис.). Докажем сначала, что четырехугольники ABEF,BCFG,CDGHи DEHAимеют общую точку. Ясно, что пересечением ABEFи CDGHявляется некоторый выпуклый четырехугольник KLMN. Отрезки AFи HCлежат внутри углов DAHи AHEсоответственно, поэтому точка Kлежит внутри четырехугольника DEHA. Аналогично доказывается, что точка Mлежит внутри четырехугольника DEHA, т. е. весь отрезок KMлежит внутри его. Аналогично отрезок LNлежит внутри четырехугольника BCFG. Точка пересечения диагоналей KMи LNпринадлежит всем нашим четырехугольникам; обозначим ее O. Разобьем восьмиугольник на треугольники, соединив точку Oс вершинами. Площадь одного из этих треугольников, например ABO, не превосходит S/8. Отрезок AOпересекает сторону KLв некоторой точке P, поэтому S_ABP$\leq$S_ABO$\leq$S/8. Так как точка Pлежит на диагонали CH, то либо S_ABC$\leq$S_ABP$\leq$S/8, либо S_ABH$\leq$S_ABP$\leq$S/8.

Ответ задачи отсутствует