Задача
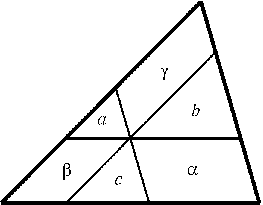
Через точку, лежащую внутри треугольника, проведены три прямые, параллельные его сторонам. Обозначим площади частей, на которые эти прямые разбивают треугольник, так, как показано на рис. Докажите, что a/$\alpha$+b/$\beta$+c/$\gamma$$\geq$3/2.
Решение
Согласно неравенству между средним геометрическим и средним арифметическим ${\frac{a}{\alpha }}$+${\frac{b}{\beta }}$+${\frac{c}{\gamma }}$$\geq$33abc/($\alpha$$\beta$$\gamma$) = 3/2, так как $\alpha$= 2$\sqrt{bc}$,$\beta$= 2$\sqrt{ca}$и $\gamma$= 2$\sqrt{ab}$(см. задачу 1.33).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет