Задача
ABCD — выпуклый четырехугольник площади S. Угол между прямыми ABи CDравен a, угол между ADи BCравен $\beta$. Докажите, что
AB . CD sin$\displaystyle \alpha$ + AD . BC sin$\displaystyle \beta$ $\displaystyle \leq$ 2S $\displaystyle \leq$ AB . CD + AD . BC.
Решение
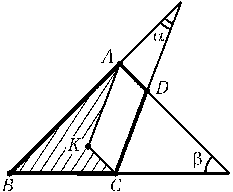
Для определенности можно считать, что пересекаются лучи BAи CD, BCи AD(рис.). Тогда, если достроить треугольник ADCдо параллелограмма ADCK, точка Kокажется внутри четырехугольника ABCD. Поэтому 2S$\geq$2SABK+ 2SBCK=AB . AKsin$\alpha$+BC . CKsin$\beta$=AB . CDsin$\alpha$+BC . ADsin$\beta$. Равенство достигается, если точка Dлежит на отрезке AC. Пусть точка D'симметрична точке Dотносительно серединного перпендикуляра к отрезку AC. Тогда 2S= 2SABCD'= 2SABD'+ 2SBCD'$\leq$AB . AD'+BC . CD'=AB . CD+BC . AD.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет