Задача
Точки C1,A1,B1взяты на сторонах AB,BC,CAтреугольника ABCтак, что BA1=$\lambda$ . BC,CB1=$\lambda$ . CA,AC1=$\lambda$ . AB, причем 1/2 <$\lambda$< 1. Докажите, что периметр Pтреугольника ABCи периметр P1треугольника A1B1C1связаны неравенствами (2$\lambda$-1)P<P1<$\lambda$P.
Решение
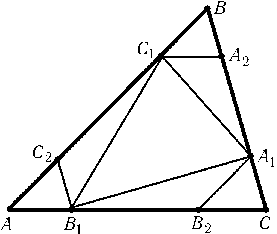
Возьмем на сторонах AB,BC,CAточки C2,A2,B2так, чтоA1B2|AB,B1C2|BC,C1A2|CA(рис.). Тогда A1B1<A1B2+B2B1= (1 -$\lambda$)AB+ (2$\lambda$- 1)CA. Аналогично B1C1< (1 -$\lambda$)BC+ (2$\lambda$- 1)ABи C1A1< (1 -$\lambda$)CA+ (2$\lambda$- 1)BC. Складывая эти неравенства, получаем P1<$\lambda$P. Ясно, что A1B1+A1C>B1C, т. е. A1B1+ (1 -$\lambda$)BC>$\lambda$ . CA. Аналогично B1C1+ (1 -$\lambda$)CA>$\lambda$ . ABи C1A1+ (1 -$\lambda$)AB>$\lambda$ . BC. Складывая эти неравенства, получаем P1> (2$\lambda$- 1)P.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь