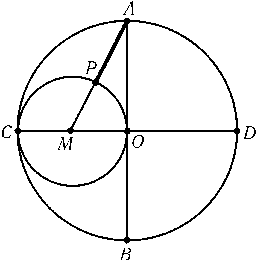
Построим окружность радиуса 1 и проведем в ней два перпендикулярных диаметра ABи CD. Пусть O — центр окружности, M — середина отрезка OC, P — точка пересечения прямой AMи окружности с диаметром OC(рис.). Тогда AM²= 1 +${\frac{1}{4}}$=${\frac{5}{4}}$, а значит, AP=AM-PM= ($\sqrt{5}$- 1)/2 = 2 sin 18^o(см. задачу 5.46), т. е. AP — длина стороны правильного десятиугольника, вписанного в данную окружность.

Ответ задачи отсутствует