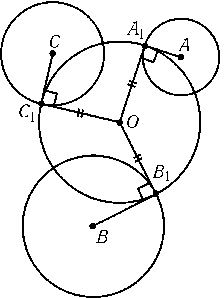
Предположим, что мы построили окружность S, касательные AA₁,BB₁и CC₁к которой имеют длины a,bи cсоответственно (A₁,B₁и C₁ — точки касания). Построим окружности S_a,S_bи S_cс центрами A,Bи Cи радиусами a,bи cсоответственно (рис.). Если O — центр окружности S, то отрезки OA₁,OB₁и OC₁являются как радиусами окружности S, так и касательными к окружностям S_a,S_bи S_c. Поэтому точка Oявляется радикальным центром окружностей S_a,S_bи S_c. Из этого вытекает следующее построение. Сначала строим окружности S_a,S_bи S_c. Затем строим их радикальный центр O. Искомая окружность является окружностью с центром Oи радиусом, равным по длине касательной, проведенной из точки Oк окружности S_a.

Ответ задачи отсутствует