Пусть H — основание высоты h_bтреугольника ABCи h_b=b. Обозначим через B'точку пересечения перпендикуляра к прямой AB, проведенного через точку A, и перпендикуляра к прямой AH, проведенного через точку C. Прямоугольные треугольники AB'Cи BAHравны, так как $\angle$AB'C=$\angle$BAHи AC=BH. Поэтому AB'=AB, т. е. точка Cлежит на окружности с диаметром AB'. Пусть S₁и S₂ — образы окружности Sс диаметром ABпри поворотах на ±90^oс центром A(рис.). Мы доказали, что точка C$\ne$Aпринадлежит объединению окружностей S₁и S₂. Обратно, пусть точка C$\ne$Aпринадлежит окружности S₁или S₂, AB' — диаметр соответствующей окружности. Тогда $\angle$AB'C=$\angle$HABи A'B=AB, поэтому AC=HB.

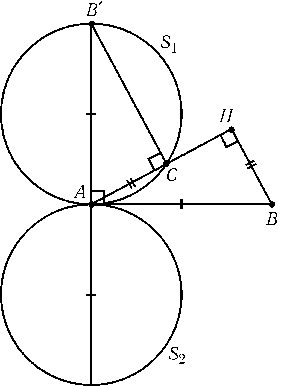
Ответ задачи отсутствует