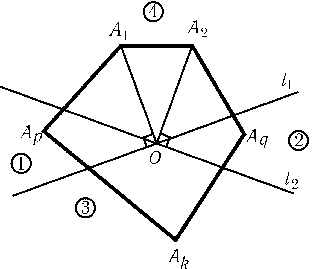
Рассмотрим две соседние вершины A₁и A₂. Если $\angle$A₁OA₂$\geq$90^o, то OA₁=OA₂, так как к основанию равнобедренного треугольника не может прилегать прямой или тупой угол. Пусть теперь $\angle$A₁OA₂< 90^o. Проведем через точку Oпрямые l₁и l₂, перпендикулярные прямым OA₁и OA₂. Обозначим области, на которые эти прямые разбивают плоскость, так, как показано на рис. Если в области (3) есть вершина A_k, то A₁O=A_kO=A₂O, поскольку $\angle$A₁OA_k$\geq$90^oи $\angle$A₂OA_k$\geq$90^o. Если же в области (3) нет вершин многоугольника, то в области (1) есть вершина A_pи в области (2) есть вершина A_q. (Если бы в одной из областей (1),(2) не было вершин многоугольника, то точка Oоказалась бы вне многоугольника.) Так как $\angle$A₁OA_q$\geq$90^o,$\angle$A₂OA_p$\geq$90^oи $\angle$A_pOA_q$\geq$90^o, то A₁O=A_qO=A_pO=A₂O. Остается заметить, что если расстояния от точки Oдо любой пары соседних вершин многоугольника равны, то равны и все расстояния от точки Oдо вершин многоугольника.

Ответ задачи отсутствует