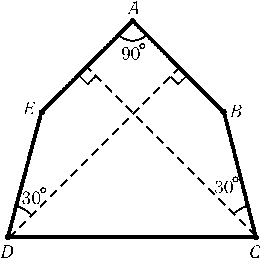
Пример пятиугольника, удовлетворяющего условию задачи, приведен на рис. Поясним, как он устроен. Возьмем равнобедренный прямоугольный треугольник EAB, проведем серединные перпендикуляры к сторонам EA,ABи на них построим точки Cи Dтак, что ED=BC=AB(т. е. прямые BCи EDобразуют с соответствующими серединными перпендикулярами углы в 30^o). Ясно, что DE=BC=AB=EA<EB<DCи DB=DA=CA=CE>EB. Докажем теперь, что пятая сторона и пятая диагональ не могут иметь общей точки. Предположим, что пятая сторона ABимеет общую точку Aс пятой диагональю. Тогда пятая диагональ — это ACили AD. Разберем эти два случая. В первом случае $\triangle$AED=$\triangle$CDE, поэтому при симметрии относительно серединного перпендикуляра к отрезку EDточка Aпереходит в точку C. Точка Bпри этой симметрии остается на месте, так как BE=BD. Поэтому отрезок ABпереходит в CB, т. е. AB=CB. Получено противоречие. Во втором случае $\triangle$ACE=$\triangle$EBD, поэтому при симметрии относительно биссектрисы угла AEDотрезок ABпереходит в DC, т. е. AB=CD. Получено противоречие.

Ответ задачи отсутствует