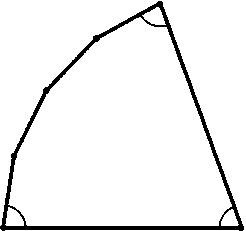
Пусть выпуклый n-угольник имеет kострых углов. Тогда сумма его углов меньше k ^. 90^o+ (n-k) ^. 180^o. С другой стороны, сумма углов n-угольника равна(n-2) ^. 180^o. Поэтому(n-2) ^. 180^o<k ^. 90^o+ (n-k) ^. 180^o, т. е. k< 4. Поскольку k — целое число, k$\leq$3. Для любого n$\geq$3 существует выпуклый n-угольник с тремя острыми углами (рис.).

Ответ задачи отсутствует