Без ограничения общности можно считать, что a_n — наибольшее из чисел a₁,...,a_n. Пусть n-угольник A₁...A_nвписан в окружность с центром O. Тогда A_iA_{i + 1}:A₁A_n= sin($\angle$A_iOA_{i + 1}/2) : sin($\angle$A₁OA_n/2). Поэтому поступим следующим образом. Из соотношения sin($\varphi_{i}^{}$/2) : sin($\varphi$/2) =a_i:a_nугол $\varphi_{i}^{}$однозначно выражается через $\varphi$, если $\varphi_{i}^{}$<$\pi$. На окружности радиуса 1 фиксируем точку A_nи рассмотрим такие переменные точки A₁,...,A_{n - 1},A_n', что $\smile$A_nA₁=$\varphi$,$\smile$A₁A₂=$\varphi_{1}^{}$,...,$\smile$A_{n - 2}A_{n - 1}=$\varphi_{n-2}^{}$и $\smile$A_{n - 1}A_n' =$\varphi_{n-1}^{}$, причем расположим эти точки двумя различными способами, изображенными на рис. (первый способ (рис., а) будет соответствовать n-угольнику, содержащему центр окружности, а второй (рис., б) — не содержащему). Остается доказать, что при изменении $\varphi$от 0 до $\pi$в одном из этих случаев точка A_n' совпадает с A_n(в самом деле, тогда с точностью до подобия получается искомый n-угольник). Предположим, что в первом случае при 0$\leq$$\varphi$$\leq$$\pi$точки A_n' и A_nникогда не совпадают, т. е. при $\varphi$=$\pi$выполняется неравенство $\varphi_{1}^{}$+ ... +$\varphi_{n-1}^{}$<$\pi$. Рисунок 6.16, бтребует некоторых комментариев: при малых углах sin$\alpha$$\approx$$\alpha$, поэтому из условия задачи следует, что при малых углах точка A_nдействительно лежит на дуге A₁A_n', так как $\varphi_{1}^{}$+ ... +$\varphi_{n-1}^{}$>$\varphi$. Итак, при малых углах $\varphi_{1}^{}$+ ... +$\varphi_{n-1}^{}$>$\varphi$, а если $\varphi$=$\pi$, то согласно предположению $\varphi_{1}^{}$+ ... +$\varphi_{n-1}^{}$<$\pi$=$\varphi$. Поэтому в некоторый момент $\varphi$=$\varphi_{1}^{}$+ ... +$\varphi_{n-1}^{}$, т. е. точки A_nи A_n' совпадают.

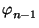
Ответ задачи отсутствует