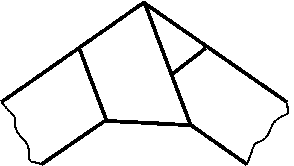
Задача
Бумажная лента постоянной ширины завязана простым узлом и затем стянута так, чтобы узел стал плоским (см. рис.).
Докажите, что узел имеет форму правильного пятиугольника.
Решение
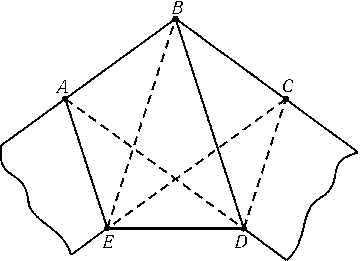
Обозначим вершины пятиугольника так, как показано на рисунке. Если в треугольнике две высоты равны, то равны и стороны, на которые опущены эти высоты. Рассматривая треугольники EAB, ABC и BCD, получаем EA = AB, AB = BC и BC = CD. Поэтому трапеции EABC и ABCD равнобедренные, то есть ∠A = ∠B = ∠C. Рассматривая треугольники ABD и BCE, получаем AD = BD и BE = CE. Так как треугольники EAB, ABC, BCD равны, то
BE = AC = BD. Поэтому AD = BE и BD = CE, то есть трапеции ABDE и CDEB равнобедренные. Следовательно, ED = AB = BC = CD = AE и
∠E = ∠A = ∠B = ∠C = ∠D, то есть ABCDE — правильный пятиугольник.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь