Задача
Докажите, что для угла Брокара$\varphi$выполняются следующие неравенства: а)$\varphi^{3}{}$$\le$($\alpha$-$\varphi$)($\beta$-$\varphi$)($\gamma$-$\varphi$); б)8$\varphi^{3}{}$$\le$$\alpha$$\beta$$\gamma$(неравенство Йиффа).
Решение
а) Рассмотрим функциюf(x) = ln(x/sin x) = ln x- lnsin x. Ясно, что функции
f'(x) = $\displaystyle {\frac{1}{x}}$ - ctgx и f''(x) = $\displaystyle {\frac{1}{\sin^2x}}$ - $\displaystyle {\frac{1}{x^2}}$
положительны при 0 <x<$\pi$. Следовательно, функцияf(x) монотонно
возрастает при возрастанииxот 0 до$\pi$и, кроме того, выпукла на этом
отрезке, т. е.
f ($\displaystyle \lambda_{1}^{}$x1 + ... + $\displaystyle \lambda_{n}^{}$xn)$\displaystyle \le$$\displaystyle \lambda_{1}^{}$f (x1) + ... + $\displaystyle \lambda_{n}^{}$f (xn)
при0$\le$xi$\le$$\pi$,0$\le$$\lambda_{i}^{}$,$\lambda_{1}^{}$+...+$\lambda_{n}^{}$= 1. В
частности,f($\varphi$)$\le$f($\pi$/6), так как$\varphi$$\le$$\pi$/6, и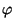
Воспользовавшись монотонностью логарифма, эти неравенства можно переписать следующим образом:
$\displaystyle \left(\vphantom{\frac\varphi{\sin\varphi}}\right.$$\displaystyle {\frac{\varphi}{\sin\varphi}}$$\displaystyle \left.\vphantom{\frac\varphi{\sin\varphi}}\right)^{6}_{}$$\displaystyle \le$$\displaystyle \left(\vphantom{\frac{\pi /6}{\sin (\pi /6)}}\right.$$\displaystyle {\frac{\pi /6}{\sin (\pi /6)}}$$\displaystyle \left.\vphantom{\frac{\pi /6}{\sin (\pi /6)}}\right)^{6}_{}$$\displaystyle \le$$\displaystyle {\frac{\varphi^3(\alpha -\varphi )(\beta -\varphi )(\gamma -\varp...
...^3\varphi\sin (\alpha -\varphi )\sin (\beta -\varphi )\sin (\gamma -\varphi )}}$.
Учитывая, чтоsin($\alpha$-$\varphi$)sin($\beta$-$\varphi$)sin($\gamma$-$\varphi$) = sin3$\varphi$,
получаем
$\displaystyle \varphi^{3}_{}$$\displaystyle \le$($\displaystyle \alpha$ - $\displaystyle \varphi$)($\displaystyle \beta$ - $\displaystyle \varphi$)($\displaystyle \gamma$ - $\displaystyle \varphi$).
б) Из неравенства$\varphi^{3}_{}$$\le$($\alpha$-$\varphi$)($\beta$-$\varphi$)($\gamma$-$\varphi$)
следует, что
64$\displaystyle \varphi^{6}_{}$$\displaystyle \le$43$\displaystyle \varphi$($\displaystyle \alpha$ - $\displaystyle \varphi$)$\displaystyle \varphi$($\displaystyle \beta$ - $\displaystyle \varphi$)$\displaystyle \varphi$($\displaystyle \gamma$ - $\displaystyle \varphi$).
Ясно также, что
4$\displaystyle \varphi$($\displaystyle \alpha$ - $\displaystyle \varphi$)$\displaystyle \le$$\displaystyle \alpha^{2}_{}$, 4$\displaystyle \varphi$($\displaystyle \beta$ - $\displaystyle \varphi$)$\displaystyle \le$$\displaystyle \beta^{2}_{}$, 4$\displaystyle \varphi$($\displaystyle \gamma$ - $\displaystyle \varphi$)$\displaystyle \le$$\displaystyle \gamma^{2}_{}$.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет