Задача
Квадрат разделен на четыре части двумя перпендикулярными прямыми, точка пересечения которых лежит внутри его. Докажите, что если площади трех из этих частей равны, то равны и площади всех четырех частей.
Решение
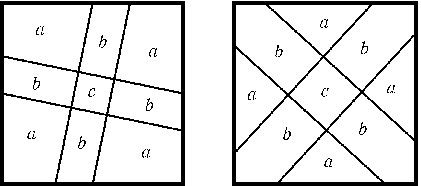
Пусть данные прямые l1и l2делят квадрат на четыре части, площади которых равны S1,S2,S3и S4, причем для первой прямой площади частей, на которые она делит квадрат, равны S1+S2и S3+S4а для второй они равны S2+S3и S1+S4. Так как по условию S1=S2=S3, то S1+S2=S2+S3. Это означает, что образ прямой l1при повороте относительно центра квадрата на +90oили -90oне просто параллелен прямой l2, а совпадает с ней. Остается доказать, что прямая l1(а значит, и прямая l2) проходит через центр квадрата. Предположим, что это не верно. Рассмотрим образы прямых l1и l2при поворотах на ±90oи обозначим площади частей, на которые они делят квадрат, так, как показано на рис. (на этом рисунке изображены оба различных варианта расположения прямых). Прямые l1и l2делят квадрат на четыре части, площади которых равны a,a+b,a+ 2b+cи a+b, причем числа a,bи cненулевые. Ясно, что три из указанных четырех чисел не могут быть равны. Получено противоречие.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь