Задача
Докажите, что диагонали AD,BEи CFописанного шестиугольника ABCDEFпересекаются в одной точке (Брианшон).
Решение
Пусть выпуклый шестиугольник ABCDEFкасается окружности
в точках R,Q,T,S,P,U(точка Rлежит на AB, Q — на BCи
т. д.).
Выберем произвольное число a> 0 и построим на прямых BCи EFточки Q'и P'так, что QQ'=PP'=a, а векторы ![]() и
и ![]() сонаправлены с векторами $\overrightarrow{CB}$и $\overrightarrow{EF}$.
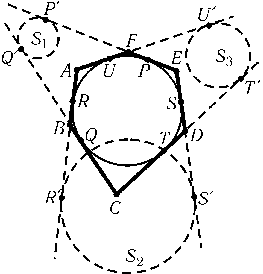
Аналогично строим точки R',S',T',U'(рис.; RR'=SS'=TT'=UU'=a).
Построим окружность S1, касающуюся прямых BCи EFв точках Q'и P'. Аналогично построим окружности S2и S3.
Докажем, что точки Bи Eлежат на радикальной оси окружностей S1и S2. BQ'=QQ'-BQ=RR'-BR=BR'(если QQ'<BQ,
то BQ'=BQ-QQ'=BR-RR'=BR') и EP'=EP+PP'=ES+SS'=ES'. Аналогично
доказывается, что прямые FCи ADявляются радикальными осями
окружностей S1и S3, S2и S3соответственно. Так как
радикальные оси трех окружностей пересекаются в одной точке,
прямые AD,BEи CFпересекаются в одной точке.
сонаправлены с векторами $\overrightarrow{CB}$и $\overrightarrow{EF}$.
Аналогично строим точки R',S',T',U'(рис.; RR'=SS'=TT'=UU'=a).
Построим окружность S1, касающуюся прямых BCи EFв точках Q'и P'. Аналогично построим окружности S2и S3.
Докажем, что точки Bи Eлежат на радикальной оси окружностей S1и S2. BQ'=QQ'-BQ=RR'-BR=BR'(если QQ'<BQ,
то BQ'=BQ-QQ'=BR-RR'=BR') и EP'=EP+PP'=ES+SS'=ES'. Аналогично
доказывается, что прямые FCи ADявляются радикальными осями
окружностей S1и S3, S2и S3соответственно. Так как
радикальные оси трех окружностей пересекаются в одной точке,
прямые AD,BEи CFпересекаются в одной точке.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь