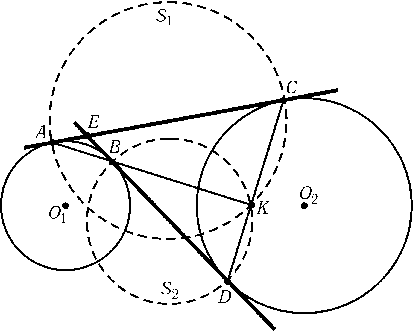
Пусть ACи BD — касательные; Eи K — точки пересечения прямых ACи BD, ABи CD; O₁и O₂ — центры окружностей (рис.). Так как AB$\perp$O₁E,O₁E$\perp$O₂Eи O₂E$\perp$CD, то AB$\perp$CD, а значит, K — точка пересечения окружностей S₁и S₂с диаметрами ACи BD. Точка Kлежит на радикальной оси окружностей S₁и S₂; остается проверить, что этой радикальной осью является прямая O₁O₂. Радиусы O₁Aи O₁Bявляются касательными к S₁и S₂, поэтому точка O₁лежит на радикальной оси. Аналогично точка O₂лежит на радикальной оси.

Ответ задачи отсутствует