Задача
На стороне BCтреугольника ABCвзята точка A'. Серединный перпендикуляр к отрезку A'Bпересекает сторону ABв точке M, а серединный перпендикуляр к отрезку A'Cпересекает сторону ACв точке N. Докажите, что точка, симметричная точке A'относительно прямой MN, лежит на описанной окружности треугольника ABC.
Решение
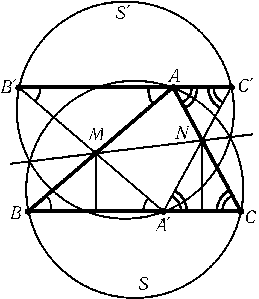
Обозначим через B'и C'точки пересечения прямых A'Mи A'Nс прямой, проведенной через точку Aпараллельно BC(рис.). Так как треугольники A'BMи A'NCравнобедренные, то $\triangle$ABC=$\triangle$A'B'C'. Поскольку AM . BM=A'M . B'M, степени точки Mотносительно окружностей Sи S', описанных около треугольников ABCи A'B'C'соответственно, равны. Это верно и для точки N, поэтому прямая MNявляется радикальной осью окружностей Sи S'. Окружности Sи S'имеют одинаковые радиусы, поэтому их радикальная ось является их осью симметрии. Точка A', лежащая на окружности S', при симметрии относительно прямой MNпереходит в точку, лежащую на окружности S.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь