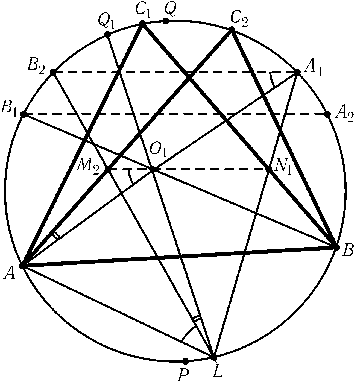
Решение этой задачи обобщает решение предыдущей задачи. Достаточно доказать, что центр O₁вписанной окружности треугольника ABC₁лежит на отрезке M₂N₁. Пусть A₁и A₂ — середины дуг BC₁и BC₂, B₁и B₂ — середины дуг AC₁и AC₂; PQ — диаметр окружности S, перпендикулярный хорде AB, причем Qи C₁лежат по одну сторону от прямой AB. Точка O₁является точкой пересечения хорд AA₁и BB₁, а точка Lкасания окружностей Sи S₁является точкой пересечения прямых A₁N₁и B₂M₂(рис.). Пусть $\angle$C₁AB= 2$\alpha$,$\angle$C₁BA= 2$\beta$,$\angle$C₁AC₂= 2$\varphi$. Тогда $\smile$A₁A₂= 2$\varphi$=$\smile$B₁B₂, т. е. A₁B₂||B₁A₂. Угол между хордами A₁B₂и BC₁равен ($\smile$B₂C₁+$\smile$A₁B)/2 =$\beta$-$\varphi$+$\alpha$, а угол между хордами BC₁и AC₂равен ($\smile$C₁C₂+$\smile$AB)/2 = 2$\varphi$+ 180^o- 2$\alpha$- 2$\beta$. Поэтому хорда M₂N₁образует с касательными BC₁и AC₂равные углы $\alpha$+$\beta$-$\varphi$, а значит, M₂N₁||A₁B₂. Предположим теперь, что точки M₂' и N₁' перемещаются по хордам AC₂и BC₁так, что M₂'N₁' ||A₁B₂. Пусть прямые A₁N₁' и B₂M₂' пересекаются в точке L'. Точка L'лежит на окружности Sлишь при одном положении точек M₂' и N₁'. Поэтому достаточно указать на дуге ABтакую точку L₁, что если M₂'',N₁'' — точки пересечения хорд AC₂и L₁B₂, BC₁и L₁A₁, то M₂''N₁'' ||A₁B₂и точка O₁лежит на отрезке M₂''N₁''. Пусть Q₁ — такая точка окружности S, что 2$\angle$(PQ,PQ₁) =$\angle$(PC₂,PC₁), и L₁ — точка пересечения прямой Q₁O₁с окружностью S. Докажем, что точка L₁искомая. Так как $\smile$B₁Q= 2$\alpha$, то $\smile$B₂Q₁= 2($\alpha$- 2$\varphi$) =$\smile$C₂A₁. Поэтому четырехугольник AM₂''O₁L₁вписанный, а значит, $\angle$M₂''O₁A=$\angle$M₂''L₁A=$\angle$B₂A₁A, т. е. M₂''O₁||B₂A₁. Аналогично N₁''O₁||B₂A₁.

Ответ задачи отсутствует