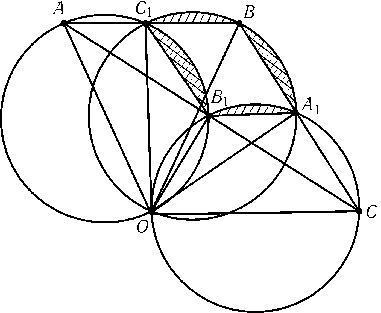
Обозначим точки пересечения окружностей, построенных на отрезках OBи OC, OAи OC, OAи OB, через A₁,B₁,C₁соответственно (рис.). $\angle$OA₁B=$\angle$OA₁C= 90^o, поэтому точки B,A₁и Cлежат на одной прямой, а так как окружности имеют одинаковые радиусы, то BA₁=A₁C. Точки A₁,B₁,C₁являются серединами сторон треугольника ABC, поэтому BA₁=C₁B₁и BC₁=A₁B₁. Так как круги имеют одинаковый радиус, то равные хорды BA₁и C₁B₁отсекают от кругов части равной площади, а равные хорды C₁Bи B₁A₁также отсекают от кругов части равной площади. Поэтому площадь криволинейного треугольника A₁B₁C₁равна площади параллелограмма A₁B₁C₁B, т. е. равна половине площади треугольника ABC.

Ответ задачи отсутствует