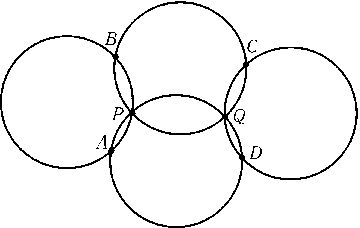
Три окружности одного радиуса проходят через точку P; A,Bи Q — точки их попарного пересечения. Четвертая окружность того же радиуса проходит через точку Qи пересекается с двумя другими в точках Cи D. При этом треугольники ABQи CDPостроугольные, а четырехугольник ABCDвыпуклый (рис.). Докажите, что ABCD — параллелограмм.