Задача
Три равные окружности пересекаются так, как показано на рис., аили б. Докажите, что $\smile$AB1+$\smile$BC1±$\smile$CA1= 180o, где знак минус берется в случае б.
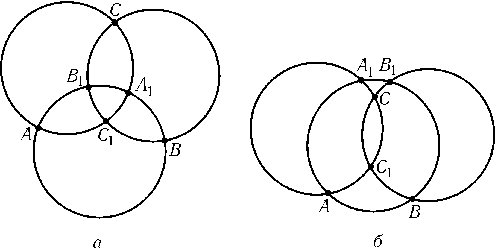
Решение
Легко проверить, что$\smile$AB1±$\smile$B1A1=$\smile$AC1+$\smile$C1A1,$\smile$BC1+$\smile$C1B1=$\smile$BA1±$\smile$B1A1и $\smile$C1A1±$\smile$CA1=$\smile$C1B1±$\smile$B1C, где знак минус берется только в случае б. Складывая эти равенства, получаем $\smile$AB1+$\smile$BC1±$\smile$CA1=$\smile$AC1+$\smile$BA1±$\smile$CB1. С другой стороны, удвоенные величины углов треугольника ABCравны $\smile$BA1±$\smile$CA1,$\smile$AB1±$\smile$CB1и $\smile$BC1+$\smile$AC1, а их сумма равна 360o.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет