Задача
Три окружности радиуса Rпроходят через точку H; A,Bи C — точки их попарного пересечения, отличные от H. Докажите, что: а) H — точка пересечения высот треугольника ABC; б) радиус описанной окружности треугольника ABCтоже равен R.
Решение
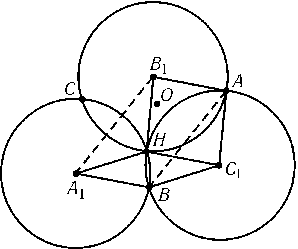
Пусть A1,B1и C1 — центры данных окружностей (рис.). Тогда A1BC1H — ромб, а значит, BA1||HC1. Аналогично B1A||HC1, поэтому B1A||BA1и B1ABA1 — параллелограмм. а) Так как A1B1$\perp$CHи A1B1||AB, то AB$\perp$CH. Аналогично доказывается, что BC$\perp$AHи CA$\perp$BH. б) Так же, как было доказано, что B1A||BA1, можно доказать, что B1C||BC1и A1C||AC1; кроме того, длины всех этих шести отрезков равны R. Достроим треугольник BA1Cдо ромба BA1CO. Тогда AB1COтоже ромб. Поэтому AO=BO=CO=R, т. e. O — центр описанной окружности треугольника ABC, и ее радиус равен R.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь