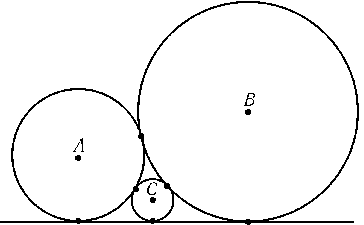
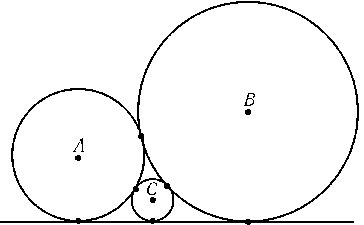
а) Пусть A1,B1и C1 — проекции точек A,Bи Cна прямую l; C2 — проекция точки Cна прямую AA1.
По теореме Пифагора CC22=AC2-AC22, т. е. A1C12= (a+c)2- (a-c)2= 4ac. Аналогично B1C12= 4bcи A1B12= 4ab. Так как A1C1+C1B1=A1B1,
то $\sqrt{ac}$+$\sqrt{bc}$=$\sqrt{ab}$,
т. е. 1/$\sqrt{b}$+ 1/$\sqrt{a}$= 1/$\sqrt{c}$.
б) Пусть A,B,C — центры к внешнихк окружностей, D — центр
к внутреннейк окружности (рис.). Полупериметр треугольника BDCравен b+c+d, поэтому
cos2$\displaystyle \left(\vphantom{\frac{BDC}{2}}\right.$$\displaystyle {\frac{BDC}{2}}$$\displaystyle \left.\vphantom{\frac{BDC}{2}}\right)$ = $\displaystyle {\frac{d(b+c+d)}{(b+d)(c+d)}}$, sin2$\displaystyle \left(\vphantom{\frac{BDC}{2}}\right.$$\displaystyle {\frac{BDC}{2}}$$\displaystyle \left.\vphantom{\frac{BDC}{2}}\right)$ = $\displaystyle {\frac{bc}{(b+d)(c+d)}}$
(см. задачу
12.13). Если $\alpha{^\prime}$+$\beta{^\prime}$+$\gamma{^\prime}$= 180
o,
то sin
2$\alpha{^\prime}$+ sin
2$\beta{^\prime}$- sin
2$\gamma{^\prime}$+ 2 sin$\beta{^\prime}$sin$\gamma{^\prime}$cos$\alpha{^\prime}$= 0
(это утверждение эквивалентно теореме косинусов). Подставив в эту
формулу значения $\alpha{^\prime}$=$\angle$
BDC/2,$\beta{^\prime}$=$\angle$
ADC/2
и $\gamma{^\prime}$=$\angle$
ADB/2, получим
$\displaystyle {\frac{bc}{(b+d)(c+d)}}$ - $\displaystyle {\frac{ac}{(a+d)(c+d)}}$ - $\displaystyle {\frac{ab}{(a+d)(b+d)}}$ + 2$\displaystyle {\frac{a\sqrt{bcd(b+c+d)}}{(a+d)(b+d)(c+d)}}$ = 0,
т. e.
$\displaystyle {\frac{a+d}{a}}$ - $\displaystyle {\frac{b+d}{b}}$ - $\displaystyle {\frac{c+d}{c}}$ + 2$\displaystyle \sqrt{\frac{d(b+c+d)}{bc}}$ = 0.
Разделив на
d, имеем $\alpha$-$\beta$-$\gamma$-$\delta$+ 2$\sqrt{\beta \gamma +\gamma {\delta}+{\delta}\beta }$= 0. Поэтому($\alpha$+$\beta$+$\gamma$+$\delta$)
2= ($\alpha$-$\beta$-$\gamma$-$\delta$)
2+ 4($\alpha$$\beta$+$\alpha$$\gamma$+$\alpha$$\delta$) = 4($\beta$$\gamma$+$\gamma$$\delta$+$\delta$$\beta$) + 4($\alpha$$\beta$+$\alpha$$\gamma$+$\alpha$$\delta$) = 2($\alpha$+$\beta$+$\gamma$+$\delta$)
2- 2($\alpha^{2}_{}$+$\beta^{2}_{}$+$\gamma^{2}_{}$+$\delta^{2}$),
т. е. 2($\alpha^{2}_{}$+$\beta^{2}_{}$+$\gamma^{2}_{}$+$\delta^{2}$) = ($\alpha$+$\beta$+$\gamma$+$\delta$)
2.