Математическая задача о параллелограмме ABCD и его вписанных окружност
Задача
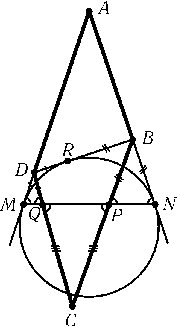
Дан параллелограмм ABCD. Вневписанная окружность треугольникаABDкасается продолжений сторон ADи ABв точках Mи N. Докажите, что точки пересечения отрезка MNс BCи CDлежат на вписанной окружности треугольника BCD.
Решение
Пусть R — точка касания вневписанной окружности со стороной BD, Pи Q — точки пересечения отрезка MNс BCи CDсоответственно (рис.). Так как $\angle$DMQ=$\angle$BPN, $\angle$DQM=$\angle$BNPи $\angle$DMQ=$\angle$BNP, то треугольники MDQ,PBNи PCQравнобедренные. Поэтому CP=CQ,DQ=DM=DRи BP=BN=BR. Следовательно, P,Qи R — точки касания вписанной окружности треугольника BCDс его сторонами (см. задачу 5.1).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет