Задача
Точка P лежит внутри треугольника ABC, причём ∠ABP = ∠ACP. На прямых AB и AC взяты такие точки C1 и B1, что BC1 : CB1 = CP : BP. Докажите, что одна из диагоналей параллелограмма, две стороны которого лежат на прямых BP и CP, а две другие стороны (или их продолжения) проходят через B1 и C1, параллельна BC.
Решение
Пусть PQRS – указанный параллелограмм (Q лежит на BP, а S – на CP). Треугольники C1BP и B1CP подобны по двум сторонам и углу между ними. Треугольники C1BQ и B1CS подобны по двум углам.
Поскольку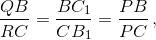 
то и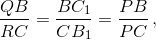 
По обратной теореме Фалеса QR || BC.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет