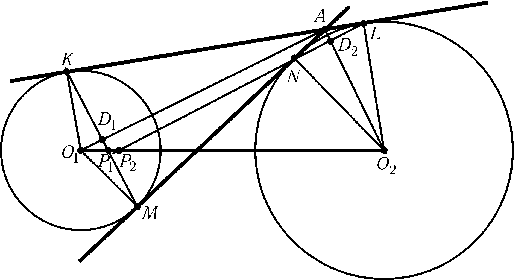
Обозначим центры окружностей через O₁и O₂. Внешняя касательная касается первой окружности в точке K, а второй окружности в точке L; внутренняя касательная касается первой окружности в точке M, а второй окружности в точке N(рис.). Пусть прямые KMи LNпересекают прямую O₁O₂в точках P₁и P₂соответственно. Надо доказать, что P₁=P₂. Рассмотрим точки A,D₁,D₂пересечения прямых KLи MN, KMи O₁A, LNи O₂Aсоответственно. $\angle$O₁AM+$\angle$NAO₂= 90^o, поэтому прямоугольные треугольники O₁MAи ANO₂подобны, а также AO₂||KMи AO₁||LN. Из параллельности этих прямых получаем AD₁:D₁O₁=O₂P₁:P₁O₁и D₂O₂:AD₂=O₂P₂:P₂O₁. Из подобия четырехугольников AKO₁Mи O₂NALполучаем AD₁:D₁O₁=D₂O₂:AD₂. Следовательно, O₂P₁:P₁O₁=O₂P₂:P₂O₁, т. е. P₁=P₂.

Ответ задачи отсутствует