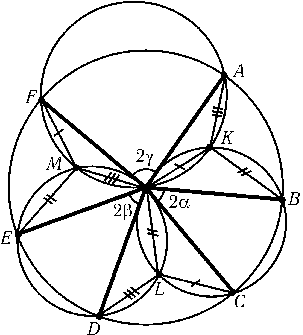
Пусть K, L, M – точки пересечения описанных окружностей треугольников FOA и BOC, BOC и DOE, DOE и FOA; 2α, 2β и 2γ – углы при вершинах равнобедренных треугольников BOC, DOE и FOA (см. рис.). Точка K лежит на дуге OB описанной окружности равнобедренного треугольника BOC, поэтому  ∠OKB = 180° – ∠OCB = 90° + α.  Аналогично  ∠OKA = 90° + γ.  Так как  α + β + γ = 90°,  то  ∠AKB = 90° + β.  Внутри правильного треугольника AOB существует единственная точка K, из которой его стороны видны под данными углами. Аналогичные рассуждения для точки L, лежащей внутри треугольника COD, показывают, что треугольники OKB и CLO равны.

  ∠COL = ∠KBO,  поэтому  ∠KOB + ∠COL = 180° – ∠OKB = 90° – α,  а значит,  ∠KOL = 2α + (90° – α) = 90° + α = ∠OKB.  Следовательно, треугольники KOL и OKB тоже равны, и  KL = OB = R.  Аналогично  LM = MK = R.

Ответ задачи отсутствует