Задача
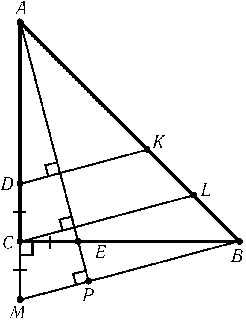
На катетах CA и CB равнобедренного прямоугольного треугольника ABC выбраны точки D и E так, что CD = CE. Продолжения перпендикуляров, опущенных из точек D и C на прямую AE, пересекают гипотенузу AB в точках K и L. Докажите, что KL = LB.
Решение
На продолжении отрезка AC за точку C возьмём точку M так, что CM = CE (см. рис.). Тогда треугольник ACE при повороте с центром C на 90° переходит в треугольник BCM. Поэтому прямая MB перпендикулярна прямой AE, а значит, параллельна прямой CL. Так как MC = CE = DC и прямые DK, CL и MB параллельны, то KL = LB.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет