Задача
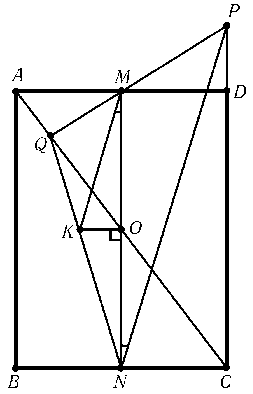
Пусть M и N – середины сторон AD и BC прямоугольника ABCD. На продолжении отрезка DC за точку D взята точка P, Q – точка пересечения прямых PM и AC. Докажите, что ∠QNM = ∠MNP.
Решение
Пусть прямая, проходящая через центр O данного прямоугольника параллельно BC, пересекает отрезок QN в точке K (см. рис.). Так как MO || PC, то
QM : MP = QO : OC, а так как KO || BC, то QO : OC = QK : KN. Следовательно, QM : MP = QK : KN, то есть KM || NP. Поэтому
∠MNP = ∠KMO = ∠QNM.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет