Задача
На плоскости расположены три окружности Ω1, Ω2, Ω3 радиусов r1, r2, r3 соответственно – каждая вне двух других, причём r1 > r2 и r1 > r3. Из точки пересечения общих внешних касательных к окружностям Ω1 и Ω2 проведены касательные к окружности Ω3, а из точки пересечения общих внешних касательных к окружностям Ω1 и Ω3 проведены касательные к окружности Ω2. Докажите, что последние две пары касательных образуют четырёхугольник, в который можно вписать окружность, и найдите её радиус.
Решение
Пусть O1, O2, O3 – центры окружностей Ω1, Ω2, Ω3 соответственно; A – точка пересечения общих внешних касательных к окружностям Ω1 и Ω3, B – к окружностям Ω1 и Ω2. Поскольку точка пересечения общих внешних касательных к двум окружностям является их центром гомотетии, то четвёртая окружность должна быть гомотетичной окружности Ω2 с центром гомотетии A и окружности Ω3 с центром гомотетии B. Поэтому её центр O должен лежать на пересечении отрезков AO2 и BO3.
Осталось найти такое число r, что окружность Ω с центром O и радиусом r гомотетична Ω2 с центром гомотетии A (то есть r : r2 = AO : AO2) и одновременно гомотетична Ω3 с центром гомотетии B (то есть r : r3 = AO : AO3). Для этого сначала найдём AO : AO2. Первый способ. Через точку A проведём прямую, параллельную O1B, до пересечения с прямой BO3 в точке T. Из подобия треугольников AO3T и O1O3B следует, что

а из подобия треугольников AOT и O2OB – что 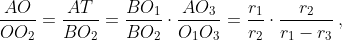
 Второй способ. Поместим в точки O1, B и A массы r2r3, r3(r1 – r2) и r2(r1 – r3) соответственно. Тогда O2 – центр масс точек O1 и B, O3 – центр масс точек O1 и A, следовательно, O1 – центр масс всех трёх точек. Значит,
Второй способ. Поместим в точки O1, B и A массы r2r3, r3(r1 – r2) и r2(r1 – r3) соответственно. Тогда O2 – центр масс точек O1 и B, O3 – центр масс точек O1 и A, следовательно, O1 – центр масс всех трёх точек. Значит, 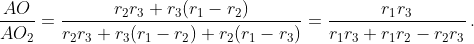 Отсюда
Отсюда 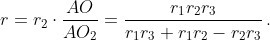 Ту же самую величину мы получим и при нахождении r из соотношения r : r3 = BO : BO3 (r2 и r3 просто поменяются местами).
Ту же самую величину мы получим и при нахождении r из соотношения r : r3 = BO : BO3 (r2 и r3 просто поменяются местами).
Ответ
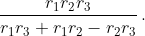
Чтобы оставлять комментарии, войдите или зарегистрируйтесь