Задача
Докажите, что противоположные стороны шестиугольника, образованного сторонами треугольника и касательными к его вписанной окружности, параллельными сторонам, равны между собой.
Решение
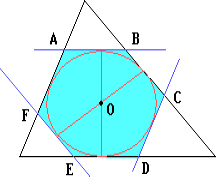
Пусть AB, CD и EF — стороны рассматриваемого шестиугольника ABCDEF, лежащие на указанных касательных. При симметрии относительно центра вписанной окружности данного треугольника прямая AB переходит в прямую DE, а прямая BC — в прямую EF. Поэтому точка B пересечения прямых AB и BC переходит в точку E пересечения прямых DE и EF.
Аналогично докажем, что при этой симметрии вершина A переходит в вершину D, а вершина F — в вершину C. Следовательно, центр окружности есть центр симметрии шестиугольника ABCDEF. Поэтому AB = ED, BC = FE и CD = FA.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь