Рассмотрим случай, когда окружности расположены одна вне другой, а данная точка лежит вне обеих окружностей. Предположим, что нужная прямая проведена. Пусть M — данная точка, S₁ и S₂ — данные окружности, O₁ и O₂ — их центры, AB и CD — равные хорды (точки A, B, C, D расположены на прямой в указанном порядке).

При параллельном переносе на вектор $\overrightarrow{CA}$ окружность S₂ перейдёт в окружность S с центром O. Прямая O₁O перпендикулярна общей хорде AB окружностей S и S₁. Проведём из данной точки M касательные MP и MQ к окружностям S₁ и S соответственно (P и Q — точки касания). По теореме о касательной и секущей

ПоэтомуMQ=MP. Пусть R — радиус окружности S₂ (и S). По теореме Пифагора из прямоугольного треугольника OQM находим, что Следовательно, точкаOлежит на окружности с центром в точкеMи радиусом, равным$\sqrt{R^{2} + MP^{2}}$. С другой стороны, т.к.$\angle$O₁OO₂= 90^o, то точкаOлежит на окружности с диаметромO₁O₂. Отсюда выстекает следующее построение. Из данной точки M проводим касательную MP к окружности S₁. Строим прямоугольный треугольник по двум катетам, равным радиусу R окружности S₁ и отрезку MP. С центром в точке M проводим окружность радиусом, равным гипотенузе построенного треугольника. Пересечение этой окружности с окружностью, построенной на отрезке с концами в центрах данных окружностей как на диаметре, даёт точку O. Наконец, через точку M проводим прямую, параллельную OO₂. Данные окружности высекают на проведённой прямой равные хорды.

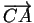
Ответ задачи отсутствует