Докажем сначала следующее утверждение. Если XY и ZY — хорды одной окружности, то образы прямых XY и ZY при поворотах в одном направлении на один и тот же угол вокруг точек соответственно X и Z пересекаются на этой окружности.

Действительно, если M — точка пересечения образов этих прямых, то либо $\angle$YXM = $\angle$YZM, либо $\angle$YXM + $\angle$YZM = 180^o. Следовательно, точки X, Y, Z и M лежат на описанной окружности треугольника XYZ.

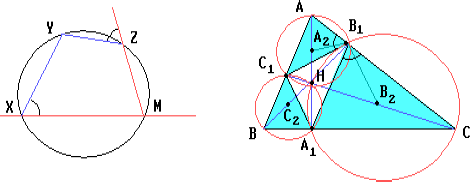
Предположим, что треугольник ABC — остроугольный. Пусть H — точка пересечения его высот AA₁, BB₁ и CC₁; A₂, B₂ и C₂ — центры описанных окружностей подобных между собой треугольников

AB₁C₁, A₁BC₁ и A₁B₁C. Точки A₂, B₂ и C₂ лежат на окружности девяти точек треугольника ABC, т.к. AH, BH и CH — диаметры описанных окружностей треугольников AB₁C₁, A₁BC₁ и

A₁B₁C, а A₂, B₂ и C₂ — центры этих окружностей.

Из подобия этих треугольников следует, что прямые B₁A₂, B₁B₂ и B₁C₂ образуют равные углы с прямыми Эйлера этих треугольников. Поскольку прямые B₁A₂, B₁B₂ и B₁C₂ пересекаются на окружности девяти точек треугольника ABC, то их образы при поворотах вокруг точек A₂, B₂ и C₂ на один и тот же угол (равный углу между каждой из них и соответствующей прямой Эйлера) также пересекаются на этой окружности.

Аналогично для случая тупоугольного треугольника.

Ответ задачи отсутствует