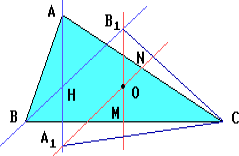
Предположим, что нужный треугольник ABC построен. Пусть O — центр его описанной окружности, AA₁ и BB₁ — высоты, лежащие на данных прямых, M и N — середины сторон BC и AC (проекции точки O на стороны BC и AC).

При симметрии относительно прямой OM прямая BB₁ переходит в прямую, проходящую через вершину C; прямая AA₁ при симметрии относительно прямой ON переходит в прямую, также проходящую через точку C.

Отсюда вытекает следующий способ построения. Через данный центр O описанной окружности проведём прямые l₁ и l₂, соответственно параллельные данным прямым. Отобразим первую из данных прямых относительно прямой l₂, а вторую — относительно l₁. Отображенные прямые пересекаются в вершине искомого треугольника.

Ответ задачи отсутствует