Треугольник  B₁AC₁ равнобедренный, его равные углы при основании  B₁C₁ острые. Поэтому их смежные углы тупые и равны между собой. Далее можно рассуждать по-разному. Первый способ. По теореме синусов   B₁C₁ : sin∠C₁BB₁ = BB₁ : sin∠BC₁B₁ = CC₁ : sin∠CB₁C₁ = B₁C₁ : sin∠B₁CC₁.  Поэтому  sin∠C₁BB₁ = sin∠B₁CC₁,  а так как углы острые, то

∠C₁BB₁ = ∠B₁CC₁.  Тогда  ∠CC₁B₁ = ∠BB₁C₁  и треугольники CC₁B₁ и BB₁C₁ равны по двум сторонам и углу между ними. Следовательно,  BC₁ = CB₁,  BA₁ = BC₁ = CB₁ = CA₁,  то есть

A₁ – середина BC.  Аналогично B₁ – середина AC, а C₁ – середина AB. Значит,  AB = 2BC₁ = 2BA₁ = BC = 2CA₁ = 2CB₁ = AC. 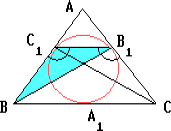Второй способ. Значит, углы ABB₁ и ACC₁ острые. В треугольниках ABB₁ и ACC₁   AB₁ = AC₁,  BB₁ = CC₁,  а угол A общий. По лемме из решения задачи 208120 эти треугольники равны,

AB = AC.  Аналогично  AB = BC.

Ответ задачи отсутствует