Задача
Из вершины B параллелограмма ABCD проведены его высоты BK и BH. Известны отрезки KH = a и BD = b. Найдите расстояние от точки B до точки пересечения высот треугольника BKH.
Решение
Первый способ.
Поскольку диагональ BD данного параллелограмма видна из точек
K и H под прямым углом, точки K и H расположены на окружности с
диаметром BD.
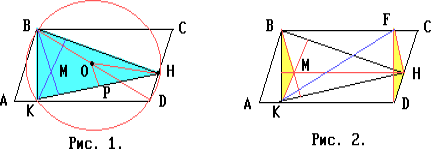
Пусть P — проекция центра O этой окружности (O — середина BD)
на сторону KH треугольника BKH, M — точка пересечения высот
треугольника BKH (рис.1). Тогда
OP = $\displaystyle \sqrt{OH^{2} - PH^{2}}$ = $\displaystyle \sqrt{\left(\frac{b}{2}\right)^{2} -
\left(\frac{a}{2}\right)^{2}}$ = $\displaystyle {\frac{\sqrt{b^{2} - a^{2}}}{2}}$.
Следовательно,BM= 2OP=$\sqrt{b^{2} - a^{2}}$.
Второй способ.
Пусть F — проекция точки D на прямую BC, M — точка
пересечения высот треугольника BKH (рис.2).
При параллельном переносе на вектор
$\overrightarrow{KD}$ точка B переходит в
точку F, а точка M — в точку H (т.к. KMHD — параллелограмм).
Поэтому треугольник FHD равен треугольнику BMK.
В прямоугольном треугольнике KHF известны катет KH = a и гипотенуза KF = BD = b (KBFD — прямоугольник). Следовательно,
BM = FH = $\displaystyle \sqrt{KF^{2} - KH^{2}}$ = $\displaystyle \sqrt{b^{2} - a^{2}}$.
Ответ
$\sqrt{b^{2} - a^{2}}$.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет