Задача
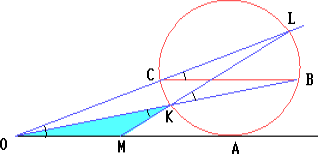
Прямая OA касается окружности в точке A, а хорда BC параллельна OA. Прямые OB и OC вторично пересекают окружность в точках K и L.
Докажите, что прямая KL делит отрезок OA пополам.
Решение
Пусть лучи AO и BC сонаправлены. Обозначим через M точку пересечения прямых AO и KL. Тогда ∠MOL = ∠BCL = ∠BKL = ∠MKO.
Поэтому треугольники MOL и MKO подобны. Следовательно, MO : ML = MK : OM, или OM2 = ML·MK.
С другой стороны, по теореме о касательной и секущей AM2 = ML·MK. Следовательно, AM = OM.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет