Задачи и олимпиады по математике

Задача

На сторонах треугольника ABC во внешнюю сторону построены подобные между собой треугольники ADB, BEC и CFA (${\frac{AD}{DB}}$ = ${\frac{BE}{EC}}$ = ${\frac{CF}{FA}}$ = k; $\angle$ADB = $\angle$BEC = $\angle$CFA = $\alpha$). Докажите, что:

середины отрезков AC, DC, BC и EF — вершины параллелограмма;
у этого параллелограмма два угла равны $\alpha$, а отношение сторон равно k.

Решение

Обозначим через $\overrightarrow{a'}$ вектор, получающийся из вектора

$\overrightarrow{a}$ поворотом на угол $\alpha$ против часовой стрелки. Известно, что

(k$\overrightarrow{a}$)' = k $\overrightarrow{a'}$ для любого числа k,

($\overrightarrow{a}$ + $\overrightarrow{b}$)' = $\overrightarrow{a'}$ + $\overrightarrow{b'}$ , и вообще, для любого числа слагаемых,

($\displaystyle \overrightarrow{a}$ + $\displaystyle \overrightarrow{b}$ +...+ $\displaystyle \overrightarrow{c}$)' = $\displaystyle \overrightarrow{a'}$ + $\displaystyle \overrightarrow{b'}$ +...+ $\displaystyle \overrightarrow{c'}$ .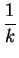

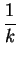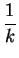Введём векторы

$\displaystyle \overrightarrow{DA}$ = $\displaystyle \overrightarrow{a}$, $\displaystyle \overrightarrow{EB}$ = $\displaystyle \overrightarrow{b}$, $\displaystyle \overrightarrow{FC}$ = $\displaystyle \overrightarrow{c}$

(рис.1). По условию задачи

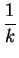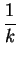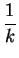$\displaystyle \overrightarrow{DB}$ = $\displaystyle {\frac{1}{k}}$ $\displaystyle \overrightarrow{a'}$ , $\displaystyle \overrightarrow{EC}$ = $\displaystyle {\frac{1}{k}}$ $\displaystyle \overrightarrow{b'}$ , $\displaystyle \overrightarrow{FA}$ = $\displaystyle {\frac{1}{k}}$ $\displaystyle \overrightarrow{c'}$ .

Поскольку

$\displaystyle \overrightarrow{AD}$ + $\displaystyle \overrightarrow{DB}$ + $\displaystyle \overrightarrow{BE}$ + $\displaystyle \overrightarrow{EC}$ + $\displaystyle \overrightarrow{CF}$ + $\displaystyle \overrightarrow{FA}$ = $\displaystyle \overrightarrow{0}$,

то

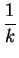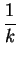- $\displaystyle \overrightarrow{a}$ + $\displaystyle {\frac{1}{k}}$ $\displaystyle \overrightarrow{a'}$ - $\displaystyle \overrightarrow{b}$ + $\displaystyle {\frac{1}{k}}$ $\displaystyle \overrightarrow{b'}$ - $\displaystyle \overrightarrow{c}$ + $\displaystyle {\frac{1}{k}}$ 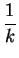$\displaystyle \overrightarrow{c'}$ = $\displaystyle \overrightarrow{0}$,

т.е.

$\displaystyle \overrightarrow{a}$ + $\displaystyle \overrightarrow{b}$ + $\displaystyle \overrightarrow{c}$ = $\displaystyle {\frac{1}{k}}$(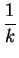 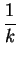$\displaystyle \overrightarrow{a'}$ + $\displaystyle \overrightarrow{b'}$ + $\displaystyle \overrightarrow{c}$) = $\displaystyle {\frac{1}{k}}$($\displaystyle \overrightarrow{a}$ + $\displaystyle \overrightarrow{b}$ + $\displaystyle \overrightarrow{c}$)'.

Обозначив$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$через$\overrightarrow{u}$, получим, что$\overrightarrow{u}$=${\frac{1}{k}}$ $\overline{u'}$ . Поскольку векторы $\overrightarrow{u}$ и $\overrightarrow{u'}$ неколлинеарны ( $\alpha$$\ne$ 0 и $\alpha$$\ne$2$\pi$), то полученное равенство возможно тогда и только тогда, когда $\overrightarrow{u}$ = $\overrightarrow{0}$. Поэтому

$\displaystyle \overrightarrow{a}$ + $\displaystyle \overrightarrow{b}$ + $\displaystyle \overrightarrow{c}$ = $\displaystyle \overrightarrow{0}$.

Далее, так какQ— середина отрезкаDCиP— середина отрезкаAC(рис.1), то$\overrightarrow{QP}$=${\frac{1}{2}}$$\overrightarrow{a}$. Аналогично$\overrightarrow{QR}$=${\frac{1}{2}}$$\overrightarrow{DB}$. ПосколькуPQ||ADиQR||BD, то$\angle$PQR=$\alpha$. Наконец,

$\displaystyle \overrightarrow{RS}$ = $\displaystyle \overrightarrow{RC}$ + $\displaystyle \overrightarrow{CF}$ + $\displaystyle \overrightarrow{FS}$ = $\displaystyle {\textstyle\frac{1}{2}}$$\displaystyle \overrightarrow{BC}$ - $\displaystyle \overrightarrow{c}$ + $\displaystyle {\textstyle\frac{1}{2}}$$\displaystyle \overrightarrow{FE}$ =

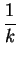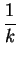
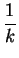= $\displaystyle {\textstyle\frac{1}{2}}$ $\displaystyle \left(\vphantom{-\overrightarrow{b} + \frac{1}{k}\overrightarrow{b'}}\right.$ - $\displaystyle \overrightarrow{b}$ + $\displaystyle {\frac{1}{k}}$ $\displaystyle \overrightarrow{b'}$ $\displaystyle \left.\vphantom{-\overrightarrow{b} + \frac{1}{k}\overrightarrow{b'}}\right)$ - $\displaystyle \overrightarrow{c}$ + $\displaystyle {\textstyle\frac{1}{2}}$ $\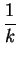displaystyle \left(\vphantom{\overrightarrow{c} - \frac{1}{k} \overline{b'}}\right.$ $\displaystyle \overrightarrow{c}$ - $\displaystyle {\frac{1}{k}}$ $\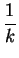displaystyle \overline{b'}$ $\displaystyle \left.\vphantom{\overrightarrow{c} - \frac{1}{k} \overline{b'}}\right)$ = - $\displaystyle {\textstyle\frac{1}{2}}$($\displaystyle \overline{b}$ + $\displaystyle \overline{c}$) = $\displaystyle {\textstyle\frac{1}{2}}$$\displaystyle \overline{a}$ = $\displaystyle \overline{QP}$.

Таким образом, четырёхугольникPQRS— параллелограмм с угломPQR, равным$\alpha$, и отношением длин сторон

$\displaystyle {\frac{PQ}{RQ}}$ = $\displaystyle {\frac{AD}{DB}}$ = k.

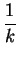
Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления