Задача
Сколько сторон может иметь выпуклый многоугольник, все диагонали которого равны?
Решение
У квадрата и правильного пятиугольника все диагонали равны. Докажем, что других выпуклых многоугольников со всеми равными диагоналями не существует.
Предположим, что все диагонали выпуклого многоугольника
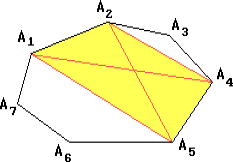
A1A2...An равны, и n $\geqslant$ 6. Рассмотрим выпуклый четырёхугольник
A1A2A4A5. Сумма его диагоналей A1A4 и A2A5 больше суммы противоположных сторон A2A4 и A1A5, что невозможно, т.к. по предположению эти суммы равны.
Ответ
4 или 5.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет