Задача
Докажите, что любая диагональ четырёхугольника меньше половины его периметра.
Решение
Пусть AC — диагональ четырёхугольника ABCD. Тогда
AC < AB + BC, AC < AD + DC.
Сложив почленно эти неравенства, получим, что
2AC < AB + BC + CD + AD.
Отсюда следует, что
AC < $\displaystyle {\frac{AB + BC + CD + AD}{2}}$.
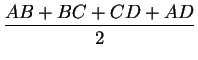
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет