Задача
Два треугольника A1B1C1 и A2B2C2, площади которых равны соответственно S1 и S2, расположены так, что лучи A1B1 и
A2B2, B1C1 и B2C2, C1A1 и
C2A2 противоположно направлены. Найдите площадь треугольника с вершинами в серединах отрезков A1A2,
B1B2, C1C2.
Решение
Пусть M, N, K — середины отрезков A1A2, B1B2, C1C2 соответственно. Треугольники A1B1C1, A2B2C2 и MNK подобны, т.к. их углы соответственно равны.
Пусть B1C1 = a1, B2C2 = a2, a2 > a1. Тогда
$\displaystyle {\frac{a_{2}}{a_{1}}}$ = $\displaystyle {\frac{\sqrt{S_{2}}}{\sqrt{S_{1}}}}$.
Поскольку отрезокKNсоединяет серединыKиNдиагоналейC1C2иB1B2трапецииB1C1B2C2, тоKN=${\frac{1}{2}}$(a2-a1). Тогда
S$\scriptstyle \Delta$MNK = $\displaystyle \left(\vphantom{\frac{KN}{B_{1}C_{1}}}\right.$$\displaystyle {\frac{KN}{B_{1}C_{1}}}$$\displaystyle \left.\vphantom{\frac{KN}{B_{1}C_{1}}}\right)^{2}_{}$S1 = $\displaystyle \left(\vphantom{\frac{a_{2} - a_{1}}{2a_{1}}}\right.$$\displaystyle {\frac{a_{2} - a_{1}}{2a_{1}}}$$\displaystyle \left.\vphantom{\frac{a_{2} - a_{1}}{2a_{1}}}\right)^{2}_{}$S1 =
= $\displaystyle {\textstyle\frac{1}{4}}$$\displaystyle \left(\vphantom{\frac{a_{2}}{a_{1} - 1} }\right.$$\displaystyle {\frac{a_{2}}{a_{1} - 1}}$$\displaystyle \left.\vphantom{\frac{a_{2}}{a_{1} - 1} }\right)^{2}_{}$S1 = $\displaystyle {\textstyle\frac{1}{4}}$$\displaystyle \left(\vphantom{ \frac{\sqrt{S_{2}}}{\sqrt{S_{1} - 1}} }\right.$$\displaystyle {\frac{\sqrt{S_{2}}}{\sqrt{S_{1} - 1}}}$$\displaystyle \left.\vphantom{ \frac{\sqrt{S_{2}}}{\sqrt{S_{1} - 1}} }\right)^{2}_{}$S1 = $\displaystyle {\textstyle\frac{1}{4}}$($\displaystyle \sqrt{S_{2}}$ - $\displaystyle \sqrt{S_{1}}$)2.
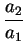
Ответ
${\frac{1}{4}}$($\sqrt{S_{1}}$ - $\sqrt{S_{2}}$)2.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет