Задача
На каждой стороне параллелограмма взято по точке. Площадь четырёхугольника с вершинами в этих точках равна половине площади параллелограмма. Докажите, что хотя бы одна из диагоналей четырёхугольника параллельна одной из сторон параллелограмма.
Решение
Пусть точки M, N, K, L лежат на сторонах соответственно AB, BC, CD и AD параллелограмма ABCD (рис. слева) и SMNKL = ½ SABCD. Способ 1. Обозначим AM = x , AL = y, BN = z, DK = t, AB = CD = a, AD = BC = b.
Тогда ½ SABCD = SAML + SBMN + SCNK + SDKL = x/a·y/b SABD + a–x/a·z/b SABC + a–t/a·b–z/b SBCD + t/a·b–y/b SACD =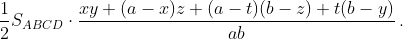 
.
Поэтому xy + (a – x)z + (a – t)(b – z) + t(b – y) = ab, или xy – xz + zt – ty = 0, или (y – z)(x – t) = 0. Отсюда x = t или y = z.
В первом случае MK || AD, во втором –
LN || AB.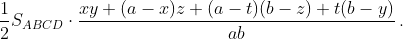 
Способ 2. (А. Эстеров) Предположим, что LN и AB не параллельны. Проведём через точку L прямую, параллельную AB, до пересечения со стороной BC в точке N1 (рис. справа). Тогда
SMN1KL = SMN1L + SN1KL = ½ (SABN1L + SLN1CD) = = ½ SABCD = SMNKL.
Поскольку треугольник MLK – общая часть четырёхугольников MNLK и MN1LK, то SMN1K = SMNK, а так как треугольники MN1K и MNK имеют общую сторону MK, то их высоты, проведённые из точек N1 и N, равны. Следовательно, MK || BC.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь