Задача
На гипотенузе и катетах прямоугольного треугольника как на
диаметрах построены полуокружности так, как показано на рисунке.
Докажите, что сумма площадей заштрихованных "луночек" равна
площади треугольника.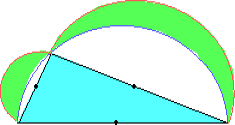
Решение
Пусть a и b — катеты треугольника, c — гипотенуза. Тогда сумма площадей указанных "луночек" равна
$\displaystyle {\frac{\pi a^{2}}{8}}$ - s1 + $\displaystyle {\frac{\pi b^{2}}{8}}$ - s2,
гдеs1иs2— площади сегментов, отсекаемых катетами от
описанного круга данного треугольника. Ясно, что
s1 + s2 = $\displaystyle {\frac{\pi c^{2}}{8}}$ - $\displaystyle {\frac{ab}{2}}$.
Следовательно, искомая сумма равна
$\displaystyle {\frac{\pi a^{2}}{8}}$ + $\displaystyle {\frac{\pi b^{2}}{8}}$ - (s1 + s3) = $\displaystyle {\frac{\pi (a^{2} + b^{2})}{8}}$ - $\displaystyle {\frac{\pi c^{2}}{8}}$ + $\displaystyle {\frac{ab}{2}}$ = $\displaystyle {\frac{\pi (a^{2} + b^{2} - c^{2})}{8}}$ + $\displaystyle {\frac{ab}{2}}$ = $\displaystyle {\frac{ab}{2}}$.

Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет