Задача
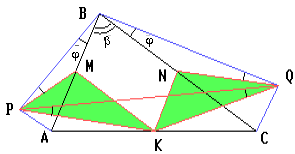
На сторонах AB и BC треугольника ABC как на гипотенузах построены вне его прямоугольные треугольники APB и BQC с одинаковыми углами величины φ при их общей вершине B. Найдите углы треугольника PQK, где K – середина стороны AC.
Решение
Пусть ∠B = β, M и N – середины сторон AB и BC треугольника ABC. Тогда KN = ½ AB = PM, KM = QN, ∠KNQ = ∠KNC + ∠CNQ = β + 2φ,
∠KMP = β + 2φ.
Следовательно, треугольники KNQ и PMK равны по двум сторонам и углу между ними. Поэтому треугольник PQK – равнобедренный. Значит,
∠PKQ = ∠PKM + ∠MKN + ∠NKQ = β + ∠PKM + ∠NKQ = β + ∠PKM + ∠MPK = β + 180° – ∠PMK = β + 180° – (β + 2φ) = 180° – 2φ, ∠QPK = ∠PQK = φ.
Ответ
180° – 2φ, φ, φ.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет