Задачи и олимпиады по математике

Задача

Сторона AD прямоугольника ABCD в три раза больше стороны AB. Точки M и N делят AD на три равные части. Найдите ∠AMB + ∠ANB + ∠ADB.

Решение

Решение 1: Предположим, что точка M расположена между точками A и N. Рассмотрим прямоугольник BPQC, равный прямоугольнику ABCD и имеющий с ним единственную общую сторону BC (см. рис.).

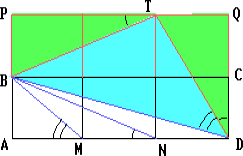
ПустьT– такая точка на сторонеPQ, что PT= 2TQ. Тогда прямоугольные треугольникиBNA, TDQиBTPравны по двум катетам. Поэтому BT = TD, ∠BTD= 180° – ∠BTP– ∠QTD= 180° – ∠BTP– (90° – ∠QDT) = 90°. Следовательно, ∠BDT= 45° и ∠AMB+ ∠ANB+ ∠ADB= ∠BDT+ ∠TDQ+ ∠ADB= 90°.

Решение 2: Так как 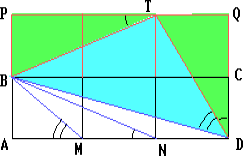то треугольники BMN и DMB подобны. Следовательно,

∠ANB + ∠ADB = ∠MNB + ∠MDB = ∠MBD + ∠MDB = ∠AMB = 45°.

Ответ

90°.

Задача

Решение

Ответ

Подтверждение удаления