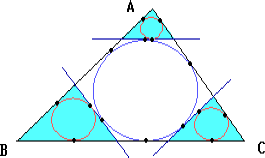
Задача
В треугольник вписана окружность радиуса r. Касательные к этой окружности, параллельные сторонам треугольника, отсекают от него три маленьких треугольника. Пусть r1, r2, r3 – радиусы вписанных в эти треугольники окружностей. Докажите, что r1 + r2 + r3 = r.
Решение
Периметр треугольника, отсекаемого прямой, параллельной стороне BC, равен сумме расстояний от точки A до точек касания вписанной в треугольник ABC окружности со сторонами AB и AC. Поэтому сумма периметров маленьких треугольников равна периметру треугольника ABC, то есть P1 + P1 + P1 = P. Из подобия треугольников следует, что r1 + r2 + r3 = r.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет