Решение 1:

  Пусть P', Q', M' и R'– точки, симметричные точкам P, Q, M и R относительно диаметра KL окружности, проходящего через точку A, E и E' – точки пересечения прямой l и окружности. Нужно доказать, что точки R' и S совпадают. Мы покажем, что и точка R', и точка S лежат на окружности, проходящей через точки C, N и P'. Такая окружность существует только одна (случай, когда какие-либо две из точек C, N и P' совпадают, очевиден), и она пересекает прямую l, кроме точки C, ещё только в одной точке.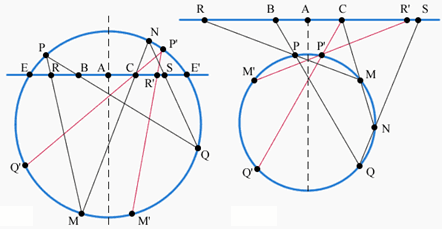

  Воспользуемсяориентированными углами.   ∠(CS, NS) = ∠(Q'Q, NQ) = ∠(Q'P, NP') = ∠(CP', NP'),  значит, точкиC, N, P', Sлежат на одной окружности.   ∠(CR', P'R') = ∠(MM', P'M') = ∠(MN, P'N) = ∠(CN, P'N),  значит, точкиC, N, P', R'лежат на одной окружности.   (Мы пользовались тем, что  Q'Q || MM' || l.  "Вырожденные" случаи, когда какие-нибудь две точки, определяющие в этих равенствах прямую, совпадают, очевидны.)

Решение 2:   Переформулируем задачу.

  Пусть P и N – две различные точки окружности с центром O, A– основание перпендикуляра, опущенного из точки O на данную прямую l, и  f – отображение, которое каждой точке X прямой l ставит в соответствие точку  f(X) этой же прямой по следующему правилу: если X' – точка пересечения прямой PX с окружностью, X'' – точка пересечения прямой NX' с l, то  f(X) – точка, симметричная X'' относительно A. Тогда отображение &nbsp:f совпадает с обратным к нему, то есть  f(f(X)) = X  для всех X (см. рис.).

  Проективную прямую, дополненную бесконечно удалённой точкой, естественно представлять себе как окружность (когда точкаXпробегает прямую, тоX'проходит полный оборот по окружности).   Если точкаXдвижется в одну сторону, то  Y = f(X) – в противоположную, поэтому отображение  fимеет две неподвижные точкиZ₁иZ₂:  f(Z₁) =Z₁, f(Z₂) =Z₂.  (Это верно для любогонепрерывноговзаимно однозначного отображения  fокружности на себя, меняющего направление обхода.)   Если точкаL– бесконечно удалённая точка прямойl, то, как нетрудно проверить,f(f(L)) =L,  причём  f(L) ≠L.  Отображение  X→f(f(X))  проективное и имеет три неподвижные точки:Z₁,Z₂иL, поэтому  f(f(X)) =X  для всехX.

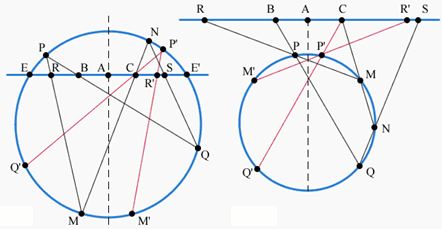
Ответ задачи отсутствует